Продолжаем говорить об алгоритмах. В прошлый раз мы обсудили метод скользящего окна, теперь двинемся дальше и поговорим о другом популярном виде задач и подходу к их решению. Он подойдёт для решения задач, где упоминаются отсортированные массивы (или связные списки), связанные с парами/тройками значений или даже подмассивами.

Как и в прошлый раз, возьмём реальную задачу с leetcode.

Задача

Leetcode: 1. Two sum

Дан массив целых чисел, необходимо вернуть индексы двух чисел, сумма которых равна заданному числу. Можно считать, что массив будет иметь ровно одно решение. Нельзя использовать одно и то же число дважды.

Аргументы: [2, 7, 11, 15], 9
Ответ: [0, 1]
Объяснение: nums[0] + nums[1] = 2 + 7 = 9

Брутфорс

Как всегда, чтобы было с чего начать, набросаем решение в лоб, со сложностью $O(n^2)$:

from typing import List


class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        for i, _ in enumerate(nums):
            for j, _ in enumerate(nums):
                if i != j and nums[i] + nums[j] == target:
                    return [i, j]
        raise Exception("the pair must be found")


if __name__ == "__main__":
    assert Solution().twoSum([2, 7, 11, 15], 9) == [0, 1]

В двух циклах мы проверяем, что индексы не совпадают и равна ли сумма двух элементов заданному, если да, то выходим. В конце бросаем исключение — в условиях задачи сказано, что пара в любом случае найдётся.

Assert не пожаловался, а значит всё работает — есть отчего отталкиваться. Но литкод не одобряет, малоприятный “Time Limit Exceeded”. Попробуем найти решение получше.

Два указателя

Для случая, когда массив чисел упорядочен, идеально подойдёт подход с двумя указателями. Сначала левый указатель указывает на начало массива, а правый на его конец. Если их сумма равна целевому значению, то мы выходим, если нет, то:

• если сумма больше целевого значения, то нам нужна меньшая сумма (логично, да?) и мы сдвигаем левее правый указатель
• если сумма меньше целевого значения, то мы сдвигаем левый указатель, чтобы её увеличить

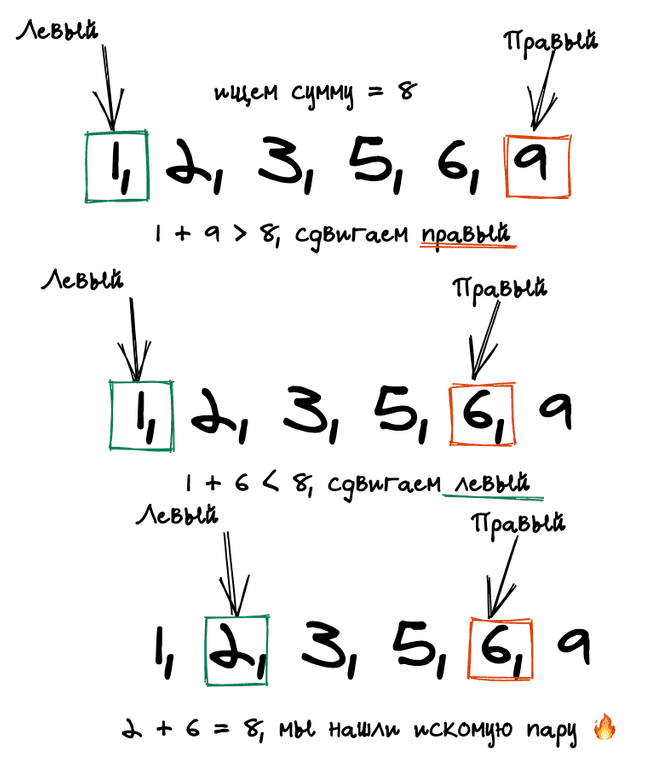
class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        left, right = 0, len(nums) - 1
        while left < right:
            cur_sum = nums[left] + nums[right]

            if cur_sum == target:
                return [left, right]
            elif target > cur_sum:
                left += 1
            else:
                right -= 1

        raise Exception("the pair must be found")


if __name__ == "__main__":
    assert Solution().twoSum([2, 7, 11, 15], 9) == [0, 1]

Всё по описанному выше алгоритму, поэтому без доп. комментариев. Мы получили сложность по времени $O(n)$ и по памяти $O(1)$.

Словарь

И давайте ещё одно альтернативное решение с линейной сложностью. При итерации по массиву, имея текущее значение, нам бы очень хотелось знать, есть ли в массиве значение, которое дополняет текущее до искомого. Это же суть задачи? Как мы можем найти его за линейное время? Верно, при помощи словаря.

class Solution:
    def twoSum(self, nums: List[int], target: int) -> List[int]:
        m = {}  # храним числа и их индексы

        # заполняем словарь
        for i, x in enumerate(nums):
            m[x] = i

        # ищем парное значение
        for i, x in enumerate(nums):
            complement = target - x

            # если существует парное значение и его индекс не равен текущему
            if complement in m and m[target - x] != i:
                return [i, m[target - x]]

        raise Exception("the pair must be found")


if __name__ == "__main__":
    assert Solution().twoSum([2, 7, 11, 15], 9) == [0, 1]

Первым делом, переносим массив в словарь, в качестве ключей — числа, а значений — их индексы. Во время второго прохода проверяем, есть ли число равное $target - x$ (элементарная математика, нам нужно же найти $x + y = target$, которое можно переформулировать в первое выражение). Если есть — отлично, если нет — идём дальше. Таким образом, имеем временную сложность $O(n)$ и сложность по памяти $O(n)$.

В этот раз не так впечатляюще, но приемлемо:

Когда использовать?

• в задаче упоминается отсортированный массив (или другая линейная структура данных), набор пар/троек элементов или подмассивы
• целевое значение должно каким-то образом получаться из пар/троек/подмассивов или должны удаляться дубликаты

Подведём итоги. Есть ряд задач, когда при увеличении одного указателя, значение другого указателя может только уменьшаться (или наоборот увеличиваться). Это позволяет нам не перебирать каждый раз все значения, а просто продолжать с последнего.